Laptops for Algernon

Exercise 1.35 Show that the golden ratio is a fixed point of  the transformation x|-> 1 + 1/x, and use this fact to compute the golden ration by means of the fixed-point procedure.

The following code works correctly.

(define (golden-ratio) (fixed-point (lambda (y) (avg y (+ 1 (/ 1 y)))) 1.0))

(golden-ratio) ; 1.6180311591702674

Exercise 1.36 Modify fixed-point so that it prints the sequence of approximations it generates, using the newline and display primitives shown in exercise 1.22.

To show each output with the newline and  display primitives, we only need to change the fixed-point method as follows:

(define (fixed-point f first-guess)
(define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
; add two methods below to the existing code.
(display guess)
(newline)
:
:

Let’s try if the newly implemented feature works:

(golden-ratio)

And we’ll get the following output:

1.0
1.5
1.5833333333333333
1.6074561403508771
1.6147785476652068
1.61702925556443
1.617723628348796
1.6179380934832117
1.6180043565683029
1.6180248320058461
1.6180311591702674

Exercise 1.36( sequel ) Find a solution to x^x = 1000 by finding a fixed point of x |-> log(1000) / log(x).

 The following code will work. In this case, we need to change the initial number to 2.0 because the base of logarithm is 2.

(define (xexp) (fixed-point (lambda (x) (/ (log 1000) (log x))) 2.0))

Then we get the following output:

2.0
5.9828921423310435
4.922168721308343
4.628224318195455
4.568346513136242
4.5577305909237005
4.555909809045131
4.555599411610624
4.5555465521473675
4.555537551999825

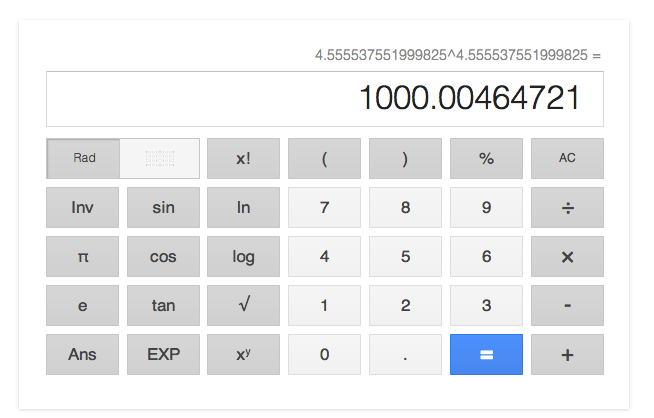
Finally we get 4.555537551999825, and we can confirm if we’ve got a correct one by means of google search.

Exercise 1.36( sequel ) Compare the number of steps this takes with and without average damping.

In the previous solution, we’ve got 46 outputs, and we still have room for improvement using average damping. Then let’s change the code( Just adding a little bit of  arithmetics will do ).

(define (xexp) (fixed-point (lambda (x) (avg x (/ (log 1000) (log x)))) 2.0))

Then the output is:

2.0
5.9828921423310435
4.922168721308343
4.628224318195455
4.568346513136242
4.5577305909237005
4.555909809045131
4.555599411610624
4.5555465521473675
4.555537551999825

The number of the output is only 10, so it looks like the correction worked.